To do this, we need to check any grid intersection points that are encountered by the ray; and see if there is a wall on the grid or not. The best way is to check for horizontal and vertical intersections separately. When there is a wall on either a vertical or a horizontal intersection, the checking stops. The distance to both intersection points is then compared, and the closer distance is chosen. This process is illustrated in the following two figures. 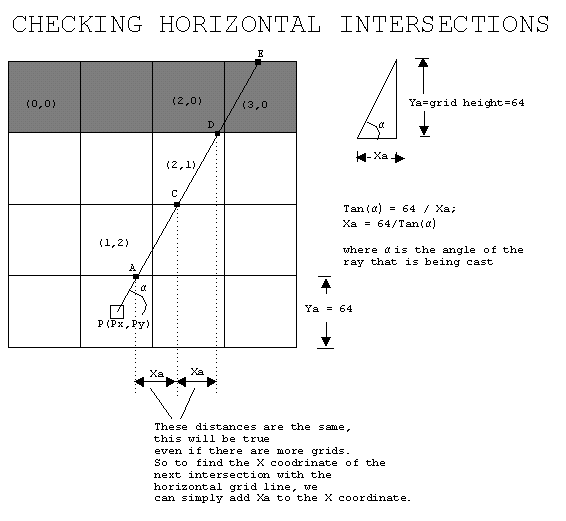Figure 15   Steps of finding intersections with horizontal grid lines: 1. 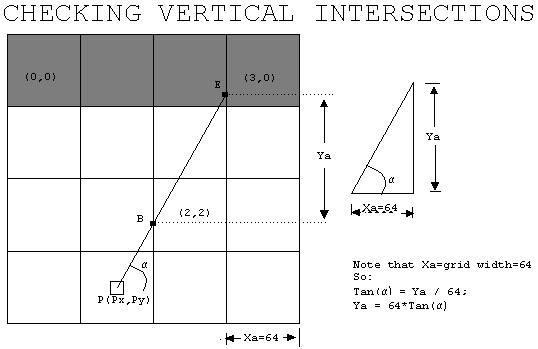Find coordinate of the first intersection (point A in this example). 2. Find Ya. (Note: Ya is just the height of the grid; however, if the ray is facing up, Ya will be negative, if the ray is facing down, Ya will be positive.) 3. Find Xa using the equation given above. 4. Check the grid at the intersection point. If there is a wall on the grid, stop and calculate te distance. 5. If there is no wall, extend the to the next intersection point. Notice that the coordinate of the next intersection point -call it (Xnew,Ynew) is Xnew=Xold+Xa, and Ynew=YOld+Ya. As an example the following is how you can get the point A: Note: remember the Cartesian coordinate is increasing downward (as in page 3), and any fractional values will be rounded down. ======Finding horizontal intersection ====== 1. Finding the coordinate of A. If the ray is facing up A.y = rounded_down(Py/64) * (64) - 1; If the ray is facing down A.y = rounded_down(Py/64) * (64) + 64; (In the picture, the ray is facing up, so we use the first formula. A.y=rounded_down(224/64) * (64) - 1 = 191; Now at this point, we can find out the grid coordinate of y. However, we must decide whether A is part of the block above the line, or the block below the line. Here, we chose to make A part of the block above the line, that is why we subtract 1 from A.y. So the grid coordinate of A.y is 191/64 = 2; A.x = Px + (Py-A.y)/tan(ALPHA); In the picture, (assume ALPHA is 60 degrees), A.x=96 + (224-191)/tan(60) = about 115; The grid coordinate of A.x is 115/64 = 1; So A is at grid (1,2) and we can check whether there is a wall on that grid. There is no wall on (1,2) so the ray will be extended to C. 2. Finding Ya If the ray is facing up Ya=-64; If the ray is facing down Ya=64; 3. Finding Xa Xa = 64/tan(60) = 36; 4. We can get the coordinate of C as follows: C.x=A.x+Xa = 115+36 = 151; C.y=A.y+Ya = 191-64 = 127; Convert this into grid coordinate by dividing each component with 64. The result is C.x = 151/64 = 2 (grid coordinate), C.y = 127/64 = 1 (grid coordinate) So the grid coordinate of C is (2, 1). (C programmer's note: Remember we always round down, this is especially true since you can use right shift by 8 to divide by 64). 5. Grid (2,1) is checked. Again, there is no wall, so the ray is extended to D. 6. We can get the coordinate of D as follows: D.x=C.x+Xa = 151+36 = 187; D.y=C.y+Ya = 127-64 = 63; Convert this into grid coordinate by dividing each component with 64. The result is D.x = 187/64 = 2 (grid coordinate), D.y = 63/64 = 0 (grid coordinate) So the grid coordinate of D is (2, 0). 6. Grid (2,0) is checked. There is a wall there, so the process stop. (Programmer's note: You can see that once we have the value of Xa and Ya, the process is very simple. We just keep adding the old value with Xa and Ya, and perform shift operation, to find out the grid coordinate of the next point hit by the ray.)   Steps of finding intersections with vertical grid lines: 1. Find coordinate of the first intersection (point B in this example). The ray is facing right in the picture, so B.x = rounded_down(Px/64) * (64) + 64. If the ray had been facing left B.x = rounded_down(Px/64) * (64) - 1. A.y = Py + (Px-A.x)*tan(ALPHA); 2. Find Xa. (Note: Xa is just the width of the grid; however, if the ray is facing right, Xa will be positive, if the ray is facing left, Ya will be negative.) 3. Find Ya using the equation given above. 4. Check the grid at the intersection point. If there is a wall on the grid, stop and calculate te distance. 5. If there is no wall, extend the to the next intersection point. Notice that the coordinate of the next intersection point -call it (Xnew,Ynew) is just Xnew=Xold+Xa, and Ynew=YOld+Ya. In the picture, First, the ray hits point B. Grid (2,2) is checked. There no wall on (2,2) so the ray is extended to E. Grid (3,0) is checked. There is a wall there, so we stop and calculate the distance. In this example, point D is closer than E. So the wall slice at D (not E) will be drawn Examples in Javascript (with source code)